Гидродинамика. Акустика
Капли: короны, всплески, звуки…
Процесс падения капель в воду, последующие течения, волны и звуки, которые люди наблюдали веками, а изучали больше столетия, теперь исследуется на качественно новом уровне. В выигрыше — теоретическая и прикладная гидродинамика, акустика и практическая метеорология.
 |
|
Трудно найти гидродинамическое явление, привлекающее большее внимание, чем всплеск, сопровождающий падение капли в воду. Практически каждый житель Земли рано или поздно попадает под дождь и, пережидая непогоду, наблюдает череду быстро сменяющихся картин: каверн от ударов капель, вырастающих из воды столбиков — коротких струек, с вершин которых вылетают капли, кольцевых волн и плавающих пузырей — признака окончания дождя. Течения, привлекающие поэтов и художников своей симметрией, красотой и быстротечностью, сопровождает специфический «шум дождя». Красоту и своеобразие всплесков, составивших основу дизайна ювелирных украшений и императорских корон, иллюстрируют многочисленные фотографии в Интернете, качество которых улучшается по мере совершенствования источников света, фото- и видеокамер.
Интерес, переживший века
Но не только красота привлекает внимание к процессам столкновений капель с поверхностью жидкости или твердого тела. Еще в Античности было замечено, что капли способны и разрушать (почву или камни), и создавать (натечные скульптуры — сталактиты и сталагмиты). «Капля точит камень не силой, но частотой падения», — считал римский писатель Публий Овидий Назон (43 г. до н.э. – 18 г. н.э.). В жестокое Средневековье каплям нашлось и бесчеловечное применение: подозреваемый, согласно закону, должен был пройти «тройное испытание» и выдержать три раза по три пытки: дыбу, кнут и «худой кувшин».
Научные исследования течений, образующихся под действием падающих в воду капель, начались в середине XIX в., когда В. Б. Роджерс, один из основателей Массачусетского технологического института (Massachusetts Institute of Technology, США), предложил несколько способов создания вихревых колец, например с помощью капель подкрашенной жидкости, которые падают в воду с умеренной высоты [1]Rogers W.B. On the formation of rotating rings by air and liquids under certain conditions of discharge // American Journal of Science and Arts. Second Series. 1858. V.26. №77. P.246–258. Несколько позднее О. Рейнольдс объяснил успокаивающее действие дождя на морское волнение уносом импульса организованного приповерхностного движения погружающимися вихрями, которые образуются в жидкости после удара капель [2]Reynolds O. On the action of rain to calm the sea // Scientific Papers on Mechanical and Physical Subjects. 1900. V.1. P.86–88.
Структурное сходство вихревых течений, в том числе значительно различающихся по масштабам, активно использовалось при решении сложных научных проблем. Основываясь на геометрическом подобии форм вихревых течений, созданных каплями в жидкости [3]Бэтчелор Дж. Введение в динамику жидкости. М., 1973. и быстро развивающихся облаков атомных взрывов в атмосфере, академик С. А. Христианович разработал эффективную методику расчета размеров радиационного следа [4]Христианович С.А., Родионов В.Н. О подъеме облака атомного взрыва. М., 1954 [отчет Акад. наук СССР, Ин-т хим. физики]. Полученные формулы были успешно подтверждены специальными лабораторными исследованиями и данными многочисленных атмосферных испытаний.
Возвращаясь к истории, следует отметить, что интерес к исследованиям всплесков капель, возродившийся (сначала в Великобритании) после длительной паузы в конце XIX в., смог опереться на новую техническую базу: для освещения быстропротекающих процессов стала использоваться искровая вспышка. Впечатляющие фотографии каверн, корон, выброшенных в воздух струек и брызг, приведенные в многочисленных статьях и книгах A. M. Вортингтона, произвели сильное впечатление на современников. Они сохраняют свою ценность до сегодняшнего дня и продолжают переиздаваться [5]Worthington A.M. The splash of the drop. Series «The romance of science». N.Y.; L., 1895 [последнее издание: Worthington A.M. The Splash of the Drop. Гамбург, 2012]. Поставленные в первых работах вопросы о механизмах формирования и величине скорости подводных течений, вызванных упавшими каплями в толще жидкости, все еще остаются без ответа.
С 40-х годов прошлого века при регистрации всплесков стали применяться лампы-вспышки — интенсивные источники света регулируемой продолжительности и яркости. В настоящее время профессиональная съемка ведется с помощью мощных светодиодных источников со световодами и цифровых фотокамер, обладающих высокой светосилой. Созданные на заре XX в. высокочувствительные приемники звука позволили изучать и акустические эффекты, сопровождающие падение капли. Первыми были зарегистрированы тональные звуковые сигналы, первоначально — в воздухе, а затем и в толще жидкости [6]Prosperetti A., Oguz H.N. The impact of drops on liquid surfaces and the underwater noise of rain // Annu. Rev. Fluid Mech. 1993. V.25. P.577–602. Развитию акустических исследований способствовал ряд причин, среди которых особое место занимали военные и экологические приложения.
Как известно, еще в начале 1940-х годов для обнаружения подводных лодок стали использоваться гидрофоны и активная гидролокация. Наблюдения показали, что один из важных источников подводного фонового акустического шума в океане — дождь. Звуки, вызванные падением как одиночных капель, так и их групп, теоретики и экспериментаторы стали активно изучать с целью оптимизации работы акустических станций [7]Franz G.J. Splashes as sources of sounds in liquids // J. Acoust. Soc. Amer. 1959. V.31. №8. P.1080–1096. В наши дни исследования подводного шума дождя призваны помочь совершенствовать технику, позволяющую дистанционно регистрировать интенсивность и определять места выпадения осадков в океане (падающие в воду снежинки также издают звук). Современные акустические комплексы дают возможность детально анализировать принятые акустические сигналы и выделять информацию о скорости ветра, характере волнения, интенсивности и местоположении областей осадков в удаленных от традиционных морских путей регионах.
Фундаментальность проблемы и разнообразие технических приложений поддерживают научный интерес к изучению и гидродинамики, и акустики всплеска. В экспериментах используется все более эффективная измерительная аппаратура, создаются феноменологические и численные модели, которые, однако, все еще не позволяют рассчитывать ключевые параметры наблюдаемых процессов.
Капель в лаборатории
Сложность описания течений, вызванных падением капли, обусловлена внутренней многомасштабностью каскада процессов, динамика и структура которых зависят от большого числа влияющих физических величин — плотностей капли ρd, принимающей среды ρt и воздуха ρa; кинематической вязкости участвующих веществ νd, νt, νa и скоростей звука csd, cst, csa; коэффициентов поверхностного натяжения на границе капли σda и принимающей жидкости σta с воздушной средой; глубины принимающей жидкости hw, высоты свободного падения H капли, ее скорости U, диаметра D и формы в момент контакта, а также от ускорения силы тяжести g. Оценки собственных пространственных и временных масштабов явления приведены в [8]Ильиных A.Ю., Чашечкин Ю.Д. Гидродинамика контакта падающей капли со свободной поверхностью жидкости // Известия РАН. Механика жидкости и газа. 2016. №2. С.3–12.
Отношения комбинаций параметров образуют характерные безразмерные комплексы — числа Рейнольдса Re = UD/νd, Фруда Fr = U2/gD, Вебера We = ρU2D/σda, Бонда Bo = ρgD2/σd2, Лапласа (или Онезорге) La = Oh-2 = Dσda/ρνD2, Маха Ma = U/csa, которые используются при систематизации экспериментальных данных. Большое число параметров, значения которых меняются в широком диапазоне, отражает сложность структуры взаимообусловленных процессов отрыва, движения, столкновения и слияния капли с принимающей жидкостью. Сложность структур и быстротечность отдельных составляющих изучаемых течений предъявляют высокие требования к чувствительности, быстродействию и разрешающей способности регистрирующей аппаратуры, которая обычно включает яркие источники света, высокоскоростные видеокамеры, микрофоны, гидрофоны, различные датчики, быстродействующие компьютеры.
Для проведения исследований в Институте проблем механики РАН был построен специальный стенд в составе комплекса уникальных исследовательских установок «ГФК ИПМех РАН» для моделирования структуры и динамики природных процессов [9]Чашечкин Ю.Д. Структура и динамика природных течений: теоретическое и лабораторное моделирование // Актуальные проблемы механики. 50 лет Институту проблем механики им. А.Ю. Ишлинского РАН. М., 2015. С.63–78. Основу стенда составил гидрооптический бассейн размером 145×50×60 см с иллюминаторами из оптического стекла. Бассейн наполнялся дегазированной водопроводной водой, глубина слоя (40 см) существенно превышала характерные масштабы наблюдаемых течений (часть опытов по визуализации течений была выполнена в прозрачных бассейнах меньшего размера).
Одиночные капли (диаметром около 0.5 см) и их последовательности создавались с помощью регулируемого дозатора. Высота свободного падения капли после отрыва от сопла дозатора устанавливалась в диапазоне от 8 до 110 см. При выбранных условиях в экспериментах наблюдался выброс толстой кумулятивной струйки, либо одиночной, либо сопровождающейся вторичным стримером — тонкой струйкой, распадающейся на цепочку мелких капель [10]Чашечкин Ю.Д., Прохоров В.Е. Структура первичного звукового сигнала при столкновении свободно падающей капли с поверхностью воды // ЖЭТФ. 2016. Т.149. №4. С.864–875. В опытах менялись диаметр капли и высота ее свободного падения, а следовательно, и скорость в момент контакта. Варьировались также и рабочие среды: изучалось взаимодействие капель чистой и соленой воды, чернил, спирта, молока, растворов солей, масла с водой и другими жидкостями.
Свободное падение капли чернил в покоящийся слой подсолнечного масла. Высота падения: 480 мм. Диаметр капли: 2,5 мм.
В отличие от ранее проведенных опытов, в которых звук регистрировался отдельно или в воздухе, или в воде, акустические измерения проводились в обеих средах одновременно с видеосъемкой картины течения. В бассейне размещался высокочувствительный измерительный гидрофон отечественной разработки с цилиндрическим чувствительным элементом и предусилителем. Для регистрации звука в воздухе применялся самодельный измерительный комплекс с микрофонной головкой.
Область наблюдений освещалась софитами и волоконными осветителями, видеорегистрация велась высокоскоростной камерой фирмы Optronis CR3000x2 с вспомогательными линзами (скорость съемки — от 2000 до 20 000 кадров/с, максимальный размер изображения 3 Мпкс).
Для управления экспериментом, синхронизации процесса сбора данных с различных датчиков, первичной обработки сигналов и подготовки данных к регистрации разработан оригинальный блок, который обеспечивал 12-разрядное аналого-цифровое преобразование, прием и передачу данных в компьютер по четырем независимым каналам с частотой до 10 МГц. Синхронизация видеоряда и фонограмм с гидрофона и микрофона производилась на стадии измерений с точностью до 1 мкс.
Совместный анализ фото, видео и фонограмм позволил выделить ряд новых деталей в картине развития течений и излучения звука при падении в воду капель воды, раствора чернил или солей металлов.
Новые образы течений
Основной элемент картины течения в ходе первичного контакта капли с принимающей жидкостью — тонкая разлетающаяся пелена, к изрезанной наружной кромке которой примыкают остроконечные стримеры (рис. 1). С вершин стримеров выбрасываются мелкие капельки, диаметры которых последовательно увеличиваются, а скорости, определяемые по длине штрихов, — падают (рис. 1,а,б). В данных опытах скорость первых вылетевших капелек брызг (20–30 м/с) на порядок и более превосходит скорость капли в момент контакта (1–2.5 м/с). Радиальные стримеры, среди которых можно выделить 10–12 главных (с шагом 25–35°) и 50–70 более мелких (с шагом 5–7°), расположены не строго регулярно. На изображении можно заметить участки с разреженными струйками («на 13 часов») и более часто расположенными («на 7 часов», рис. 1,а).
Отмеченные особенности картины течения сохраняются и при падении капли чернил в воду. Внешний край разлетающейся кольцевой пелены также рассечен системой радиальных стримеров, соединенных вогнутыми дужками (рис. 1,б). Быстро вылетающие из области контакта капельки всегда включали обе слившиеся жидкости и оказывались окрашенными при падении и капли чернил в воду, и капли воды в чернила.

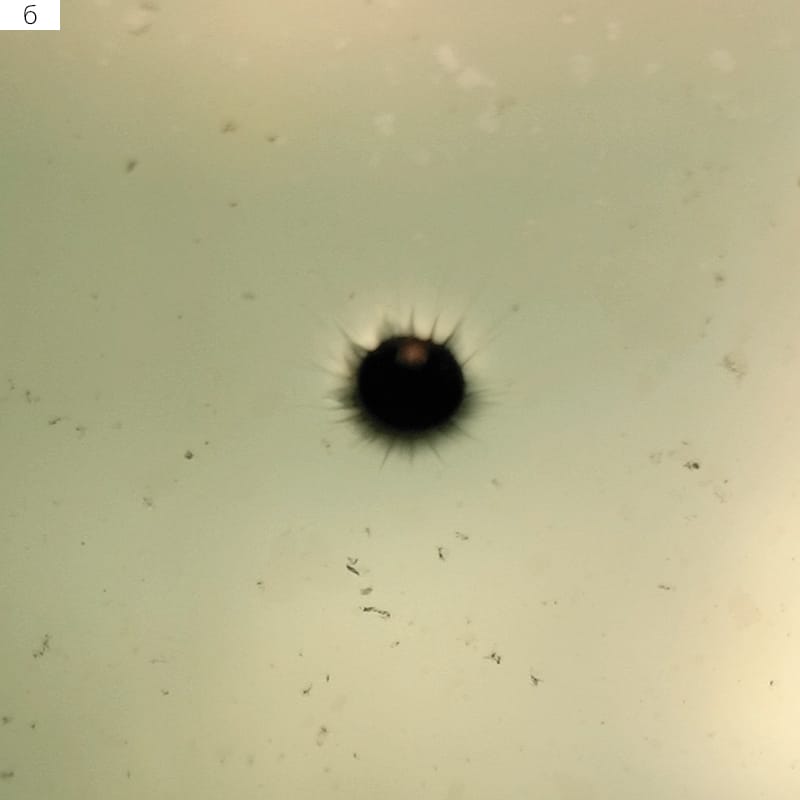
Мелкие брызги и пелена сначала вылетали непосредственно из области контакта капли с принимающей жидкостью; после того как ее нижняя половина полностью сливалась с поверхностью, а линия контакта погружалась ниже уровня жидкости, они продолжали извергаться с вершин зубцов окружающего каверну кольцевого ребра — выступающего над невозмущенной поверхностью венца (рис. 2,а,б). Размер выбрасываемых капелек постепенно увеличивался по мере сглаживания вершин зубцов на верхней кромке венца. Тыльная сторона погружающейся капли оставалась гладкой: при увеличении на изображении отчетливо прорисовываются ровные линии масштабной сетки, расположенной на дне бассейна (рис. 2,а).

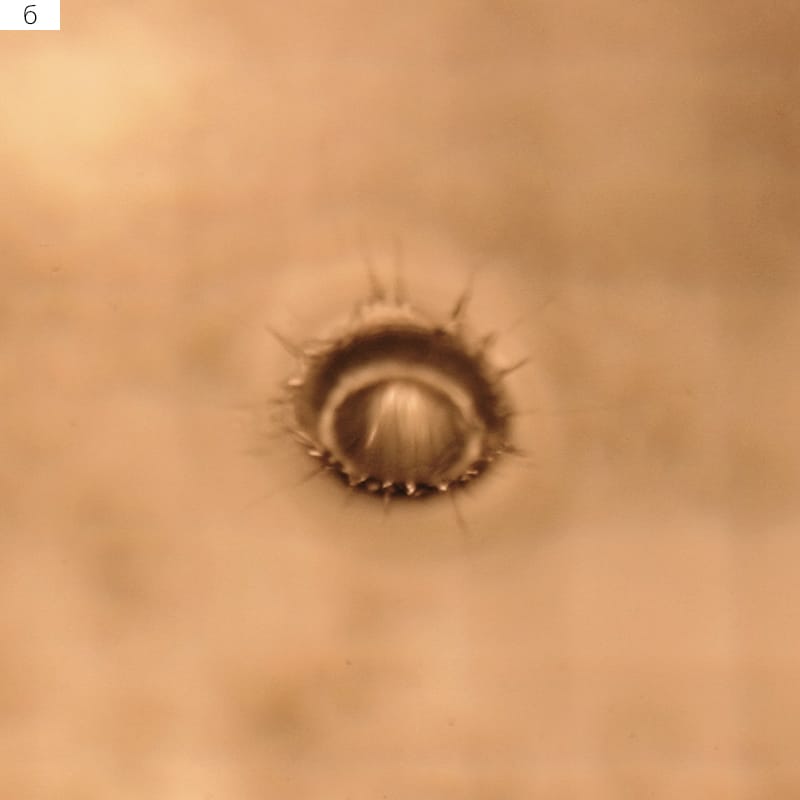
Однако гладкость боковой поверхности капли для некоторых пар жидкостей нарушается — на ней наблюдаются группы коротких капиллярных волн, вызванных падением мелких капелек, которые вылетают с зубцов венца. Если в воду погружается капля воды, число таких событий невелико (рис. 3,а), зато у капли раствора поваренной соли боковая поверхность оказывается полностью покрытой группами капиллярных волн (рис. 3,б).
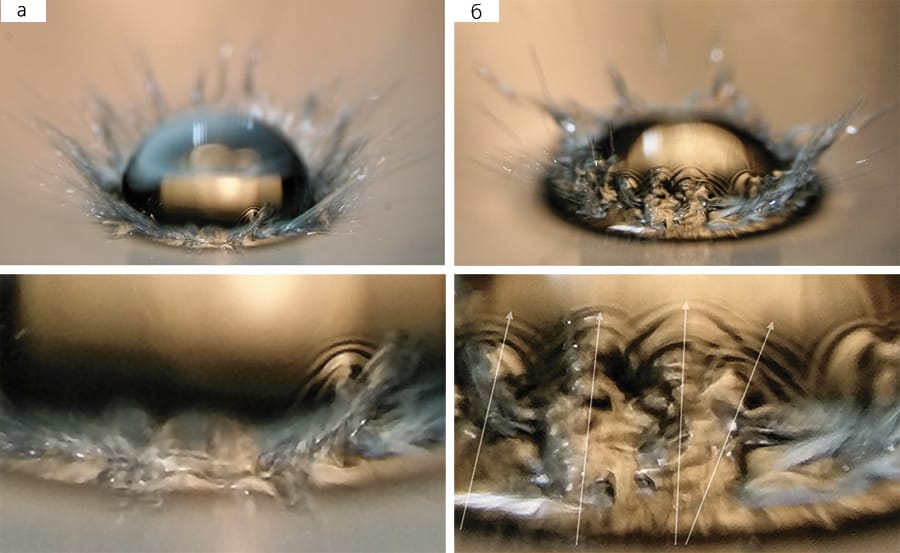
Факт попадания брызг на погружающуюся каплю указывает на заметное влияние относительной разности значений коэффициентов поверхностного натяжения Rσ = (σta – σda)/(σta + σda), которая отражает различия плотности поверхностной энергии сливающихся жидкостей в области контакта [8]Ильиных A.Ю., Чашечкин Ю.Д. Гидродинамика контакта падающей капли со свободной поверхностью жидкости // Известия РАН. Механика жидкости и газа. 2016. №2. С.3–12. При слиянии жидкостей, когда свободная поверхность исчезает, потенциальная поверхностная энергия, сосредоточенная в слое толщиной порядка размеров молекулярного кластера (~10-6 см), освобождается и переходит в другие формы — внутреннюю и кинетическую энергии течений жидкости. Большая плотность энергии в тонком слое в окрестности границы контакта двух сред влияет на формирование общей картины течения и характер переноса вещества капли в воздухе, в приповерхностном слое и в толще принимающей жидкости.
По традиции, заложенной еще первыми публикациями [5]Worthington A.M. The splash of the drop. Series «The romance of science». N.Y.; L., 1895 [последнее издание: Worthington A.M. The Splash of the Drop. Гамбург, 2012]. большинство иллюстраций всплеска и в настоящее время [6]Prosperetti A., Oguz H.N. The impact of drops on liquid surfaces and the underwater noise of rain // Annu. Rev. Fluid Mech. 1993. V.25. P.577–602. получены при горизонтальном положении линии визирования (рис. 4). В такой проекции стенка каверны и внешняя поверхность венца в фазе роста выглядят окрашенными плотно и равномерно. Однако в центральной части изображения на внутренних стенках венца можно все же различить отдельные окрашенные волокна (рис. 4,а). На более поздней стадии расплывания венца каверна деформируется сбегающими капиллярными волнами и приобретает ступенчатую форму (рис. 4,б). Ее поверхность остается окрашенной плотно и равномерно. Со стенок каверны в толщу жидкости вторгаются тонкие струйки, головки которых трансформируются в небольшие вихревые колечки.
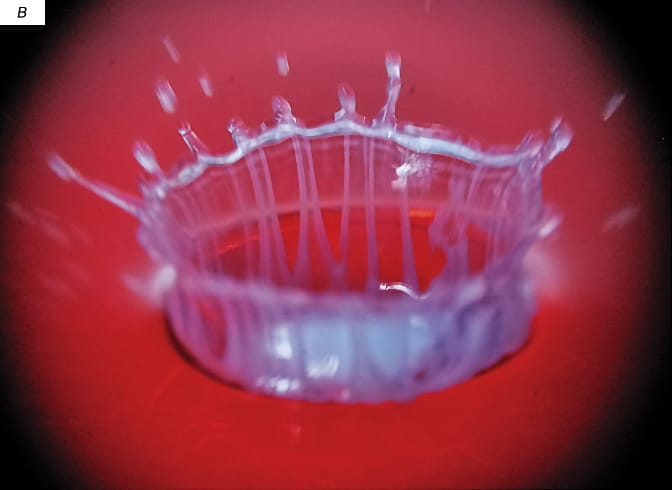
Более детально представить, как вещество окрашенной капли распределяется по поверхности венца и каверны, позволяют фотографии (рис. 5), отражающие процесс в динамике. На фоне сплошной поверхности жидкости окрашенное вещество капли оказывается сосредоточенным в тонких полосках (волокнах) различной толщины, образующих линейчатые структуры на поверхности каверны и выступающего венца. Но по мере того как венец растет, стабилизируется и расплывается, обнаруживаются и различия в картинах распределения окрашенного вещества капли по поверхности принимающей жидкости.


В фазе роста венца часть окрашенных волокон подходит к выступающим зубцам, часть — к впадинам на кромке (шевроне) венца, которая постепенно становится более плотно окрашенной, чем его стенки (рис. 5,а). Группы вылетающих с вершин различных зубцов капель располагаются внутри колец, разделенных пустыми промежутками. Боковая поверхность венца оказывается покрытой короткими капиллярными волнами, бегущими от шеврона к центру каверны. В начальной стадии контуры гребней и впадин волн отражают форму источника — шеврона. При этом фазовые поверхности коротких капиллярных внутренних волн пересекаются ниже зубцов под углом (рис. 5,а). Появление вогнутых участков на внешней кромке венца отражает угловую неоднородность распределения скорости жидкости в венце, природа формирования которой нуждается в дальнейшем изучении.



В фазе стабилизации высоты венца линейчатый характер распределения окраски сохраняется, но наряду с узкими штрихами на увеличенном изображении можно видеть и диффузно окрашенные широкие полосы (рис. 5,б). Фазовые поверхности капиллярных волн смыкаются в единую кольцевую систему.
В стадии расплывания на поверхности венца помимо первоначальных линейчатых структур проявляются сверхтонкие волокна и группы сверхкоротких капиллярных волн (рис. 5,в). При этом картина основной группы кольцевых капиллярных волн выравнивается, но характер распределения вещества капли по поверхности венца остается дискретным.
Качественные особенности картины течения — периодичность вылета брызг с вершин стримеров, линейчатый характер распределения вещества капли по поверхности венца — сохраняются и при погружении капли молока в воду, подкрашенную красными чернилами (рис. 6). Здесь стенка раскрытого наружу венца более тонкая, чем у капли воды на рис. 5, стримеры редкие и острые, вылетающие брызги быстрые, на что указывает длина штрихов на рис. 6,а. Полосчатые структуры располагаются на стенках и венца, и каверны, где они контактируют с плотно окрашенным остатком погружающейся капли.


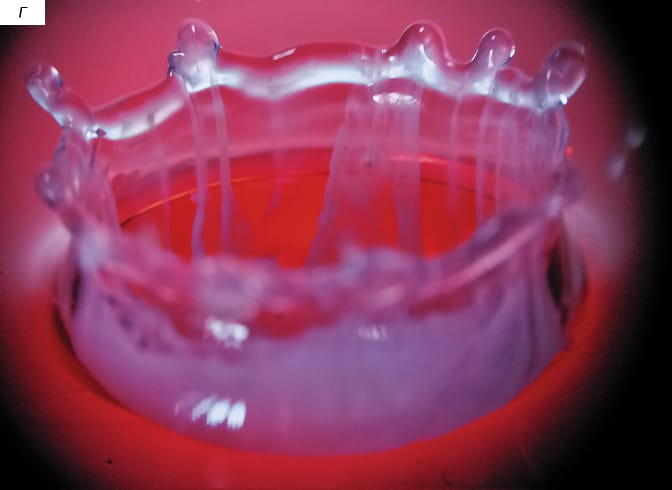
Длина волокон растет в фазе углубления каверны и роста венца, который постепенно, по мере выпрямления стенок, принимает цилиндрическую форму (рис. 6,б). При этом увеличивается степень изрезанности его шеврона. Вследствие расщепления толстых прядей на тонкие волокна растет и число волокон, которые не прерываются на всей боковой поверхности венца. Окрашенные полоски на стенках каверны расширяются в области контакта с остатком погружающейся капли. В картине распределения брызг отчетливо выделяется кольцевая щель между последовательно вылетающими группами капелек.
В стадии максимальной высоты верхняя кромка венца начинает утолщаться и стягиваться внутрь под действием сил поверхностного натяжения (рис. 6,в). На дне каверны просматриваются остатки капли молока. Зубцы также утолщаются, с их вершин вылетают все более крупные и медленные капельки. Волоконные структуры прослеживаются по всей высоте поверхности венца.
В начале стадии спадания венца его наружная поверхность в нижней части оказывается покрытой сплошным слоем молока (рис. 6,г). Однако на внутренней поверхности по-прежнему прослеживаются отдельные волокна — как изолированные, так и собранные в группы. Волокна доходят до остатков расплывающихся зубцов и свернутой наружной кромки.
Несколько иной вид имеют распределения растворимой краски и молока по дну каверны (рис. 7). Окрашенные молоком волокна вокруг остатка погружающейся в воду капли молока образуют на дне каверны сетку с выраженной зональной структурой (рис. ,а), внешний ряд которой на стенках венца состоит из вытянутых волокон. Следующий кольцевой ряд, лежащей уже на дне каверны, составляют вытянутые четырехугольники, которые контактируют с менее регулярными элементами — четырех- и пятиугольниками. Последний ряд примыкает к кусочно-гладкой границе остатка капли.

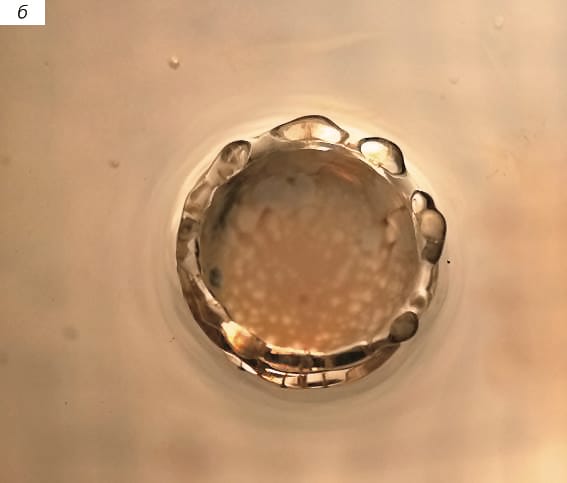
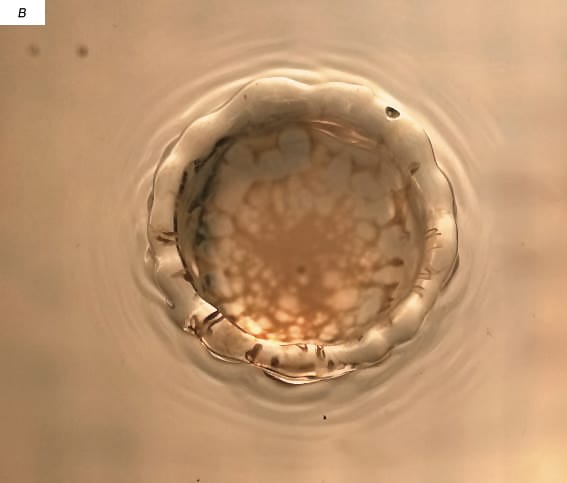
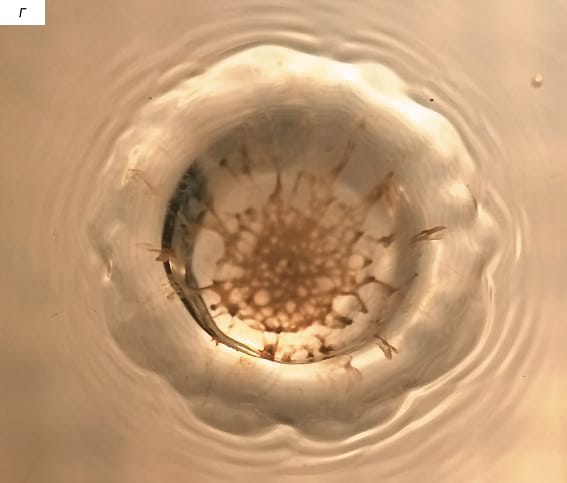
После полного погружения остатка капли все дно каверны оказывается покрытым сеткой, в которой выделены несколько кольцевых ярусов многоугольников, включающих треугольные, четырехугольные и пятиугольные элементы. Длина волокон — границ ячеек сетки — лежит в диапазоне от 0.3 до 1.3 мм и убывает к центру течения (рис. 7,б). Толщина волокон составляет 0.24 мм на нижнем и 0.47 мм на верхнем ярусе, размеры ячеек — от 0.3 до 2 мм. По мере роста каверны и расплывания венца увеличиваются и размеры ячеек внешнего ряда (рис. 7,в). Отдельные окрашенные прослойки видны и на внешней кромке венца.
Сетка, образованная окрашенными молоком волокнами, сохраняется и в фазе растекания венца (рис. 7,г), причем даже здесь отдельные волокна прослеживаются вплоть до шеврона (в верхней части изображения). Неровная наружная поверхность венца окружена системой капиллярных волн, формы гребней которых повторяют контуры линии контакта венца с принимающей жидкостью.




Дальнейшее усложнение картины течения наблюдается в фазе расплывания венца и формирования центральной кумулятивной струи, с вершины которой выбрасывается одна или несколько вторичных капель. Детали тонкой структуры течения позволяют визуализировать наблюдения при различных положениях линии визирования. На фотографии в традиционной ориентации (сбоку и сверху) видно, что наклонная поверхность пьедестала вырастающей струйки, с вершины которой выбрасывается капля, выглядит шероховатой с полосчатой ребристой микротекстурой (рис. 8,а). Угловатая форма светлой линии, окружающей конический пьедестал, указывает на отсутствие непрерывной аксиальной симметрии течения. На неровном дне остатка каверны округлые впадины разделяют заостренные гребни. Фазовые поверхности расходящихся капиллярных волн рассечены разрывами, располагающимися вдоль радиальных и наклонных линий.
Капля, вылетающая с вершины струйки, сравнима по объему с исходной, падающей в жидкость. Круговая линия контура центральной капли располагается в центре пятиугольника с выраженными ребрами, как показывает рис. 8,б (вид снизу). Угловатость форм сохраняется и в контурах ближайших к струйке коротких капиллярных волн, и на более удаленных, располагающихся на остатке венца.
Растущую кумулятивную струю, плотно окрашенную чернилами капли, окружает достаточно регулярная система из семи двойных радиальных струек, завершающихся небольшими окрашенными колечками. Под пьедесталом струи располагается система наклонных вихревых петель, плотность которых увеличивается по мере приближения к ее границе (рис. 8,в). Непосредственно под кумулятивной струйкой окрашенная жидкость образует сложную систему наклонных струек и петель (рис. 8,г). Обращает внимание отличие четких форм элементов течения в воздушной среде и сложное распределение окрашенной жидкости капли в толще жидкости.
В последнем случае в поле зрения фотоаппарата одновременно со струйкой попадает и изображение свободной поверхности, которое приводится в нижней части рис. 8,г. Здесь выделены светлая линия контакта струйки с ложбиной, протяженные вершины ребер и темные впадины, а также отдельные окрашенные струйки неправильной формы и сложная система капиллярных волн.
Сопутствующий саундтрек
Анализ синхронизованных аудио- и видеограмм показал тесную связь гидродинамических и акустических процессов, инициированных падением капли в жидкость. Излучение звуковых пакетов привязано к максимальным значениям ускорения движения границы каверны и отрыву газовых полостей (рис. 9).
Сопоставим временные зависимости глубины z, скорости vz и ускорения a движения кромки дна каверны (кривые 1–3 в верхней части рис. 9) с фонограммой гидрофона (нижняя часть рисунка): оказывается, излучение звуковых пакетов синхронизовано с резким увеличением ускорения. В данном эксперименте наблюдается два экстремума скорости и ускорения при t = 163 и 198 мс, с которыми синхронизованы два звуковых пакета (II и III), следующие за ударным импульсом I.
Ударный импульс I на фонограмме рис. 9, который излучается в момент первичного контакта капли с поверхностью (врезка а), имеет нерегулярный характер, его уровень и частота существенно меняются от опыта к опыту. На спадающем участке сигнал осциллирует с частотой, монотонно уменьшающейся в диапазоне от 110 до 80 кГц (вставка во врезке а). Далее в течение продолжительного интервала (до 150 мс) заметная акустическая активность отсутствует.

Глубина каверны, отсчитываемая от уровня невозмущенной поверхности до нижней точки каверны, плавно растет в процессе слияния капли, а затем так же плавно уменьшается (кривая 1). Наблюдаемые осцилляции связаны с моментами, когда над гидрофоном проходят гребни/впадины капиллярных волн и остаток венца.
Вслед за стадией роста кумулятивной струи, отрыва капли с ее вершины и погружения в жидкость (где сохраняются ранее сформировавшиеся приповерхностные течения) следует формирование новой каверны, повторяющей в общих чертах эволюцию первичной. Ее глубина (кривая 1), скорость и ускорение также меняются плавно, и, как следует из видеограммы, каверна сохраняет свою целостность.
Резкое уменьшение глубины каверны, когда скорость и ускорение достигают значений 1.5 м/с и 1 км/с2 соответственно, происходит в конце данной фазы при t = 168 мс. На видеокадрах в этот момент наблюдается разрыв цилиндрической перемычки, связывающей газовый пузырь с каверной, в ходе которого формируются быстро исчезающие конические заострения. Одновременно на фонограмме гидрофона возникает звуковой пакет II, амплитуда которого монотонно спадает в течение 3 мс (врезка б). В спектре сигнала доминирует частота 4 кГц (вставка на врезке б). Излучение звука прекращается, когда полость приобретает сглаженную форму.
Погружающаяся вторичная капля порождает новую каверну, от дна которой в момент резкого увеличения скорости (до 3 м/с) и ускорения (до 2 км/с2) при t = 197 мс отделяется следующая газовая полость. В этот же момент на фонограмме появляется пакет III продолжительностью 3 мс (врезка в), с основной частотой 11 кГц и менее выраженным пиком на 4.5 кГц (вставка на врезке в).
Глазами теоретика
Особенности действия механизма выброса стримеров и быстрых брызг, формирования линейчатых картин распределения вещества капли по поверхности каверны и венца, возбуждения колебаний отрывающихся газовых полостей поясняет анализ фундаментальной системы уравнений механики жидкостей [10]Чашечкин Ю.Д., Прохоров В.Е. Структура первичного звукового сигнала при столкновении свободно падающей капли с поверхностью воды // ЖЭТФ. 2016. Т.149. №4. С.864–875. Входящие в нее уравнения описывают перенос вещества (плотности ρ и массы M), вектора импульса p, концентрации растворенных веществ Ni и полной энергии Etot, которая включает кинетическую энергию движения Ekin, потенциальные энергии Epot = Eσ + Eg (гравитационную Eg и поверхностную Eσ = σtaΔS, вариация которой обусловлена изменением площади свободной поверхности ΔS), а также внутреннюю энергию ε [11]Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.6: Гидродинамика. М., 2006. Все базовые переменные независимы и характеризуются собственными пространственными картинами.
Анализ фундаментальной системы с учетом условия совместности, определяющего ее ранг, показывает, что течения характеризуются обширными наборами пространственных и временных масштабов, значения которых зависят от свойств среды (плотности, вязкости, диффузии компонент), вида, геометрии и энергетики течений [12]Chashechkin Yu. D. Differential fluid mechanics — harmonization of analytical, numerical and laboratory models of flows // Mathematical Modeling and Optimization of Complex Structures. Springer Series «Computational Methods in Applied Sciences». 2016. V.40. P.61–91. Чтобы дать представление о сложности задачи, перечислим взаимосвязи между различными величинами.
В полном описании среда, наряду с динамическими уравнениями, характеризуется термодинамическим потенциалом, производные которого определяют физические величины (плотность, давление, температуру и др.). В данной задаче удобно использовать свободную энтальпию (потенциал Гиббса G). Дифференциал потенциала G в толще однородной жидкости I dGI = –sdT + VdP определяется локальными дифференциалами температуры T и давления P, здесь s — энтропия, V = 1/ρ — удельный объем, ρ — плотность (рис. 10,а). В многокомпонентной среде потенциал Гиббса дополнительно зависит от μi — химического потенциала и dNi — концентрации i-го вещества: dG = –sdT + VdP + μidNi.
При подходе к границе фаз в приповерхностном слое II толщиной порядка размера молекулярного кластера δc ~ 10-6 см анизотропия сильных атомно-молекулярных взаимодействий порождает как силы поверхностного натяжения, минимизирующие площадь поверхности капельных жидкостей Sf, так и доступную потенциальную поверхностную энергию Eσ = σSf, которую учел Дж.Гиббс в выражении для свободной энтальпии dGII = –sdT + VdP + σdSf еще в конце XIX в. [13]Гиббс Дж.В. О равновесии гетерогенных веществ. Термодинамические работы. М.; Л., 1950.
Непосредственно на границе жидкой и газовой фазы III толщиной в несколько молекулярных слоев δm ~ 10-8 см несбалансированность взаимодействий настолько велика, что может вызвать расщепление молекул воды на ионные составляющие. Такая среда дополнительно характеризуется собственными химическими потенциалами компонент μk с дифференциалами концентраций dNk в выражении для потенциала Гиббса dGIII = –sdT + VdP + μkdNk + σdSf. Состав и распределение веществ и зарядов на поверхностях соприкасающихся сред, в частности воды и воздуха, пока изучены недостаточно полно.
Что же показывают расчеты?
Падающая капля (с параметрами ρ, M, p, Etot = Ekin + ε + Eσ), которая вносит в принимающую среду вещество, импульс и энергию (кинетическую Ekin, внутреннюю ε и доступную потенциальную поверхностную Eσ), формирует комплекс взаимообусловленных процессов. Кинетическая энергия Ekin = MU2/2 и импульс pd = MU, равномерно распределенные в объеме капли V = πD3/6, вносятся в принимающую жидкость пропорционально погруженному объему. При этом вертикальная компонента импульса быстро убывает, поскольку энергия движения расходуется на формирование течений и увеличение гравитационной потенциальной энергии в возмущенной среде.
Сравнения величин кинетической и поверхностной потенциальной энергии капли воды диаметром D = 0.42 см, падающей в воду со скоростью U = 2.5 м/с, показывают, что основную долю (более 97%) составляет кинетическая энергия движения (Ekin = 120 мкДж, потенциальная поверхностная энергия Eσ = 4 мкДж, Ekin/Eσ = 30). Однако плотность доступной потенциальной поверхностной энергии Wσ = 3·106 Дж/м3 существенно выше, чем кинетической Wkin = 3·103 Дж/м3, Wkin/Wσ = 10-3 в силу ее концентрации в тонком слое II.
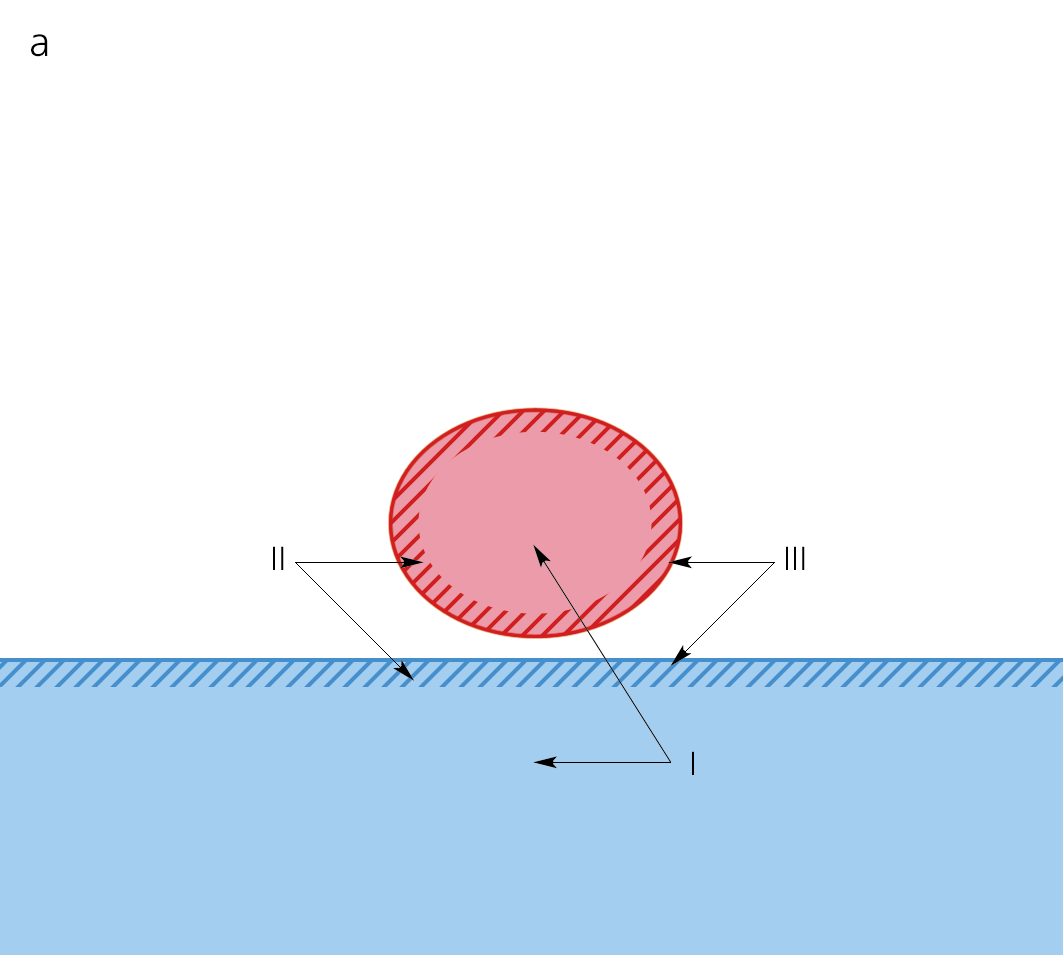
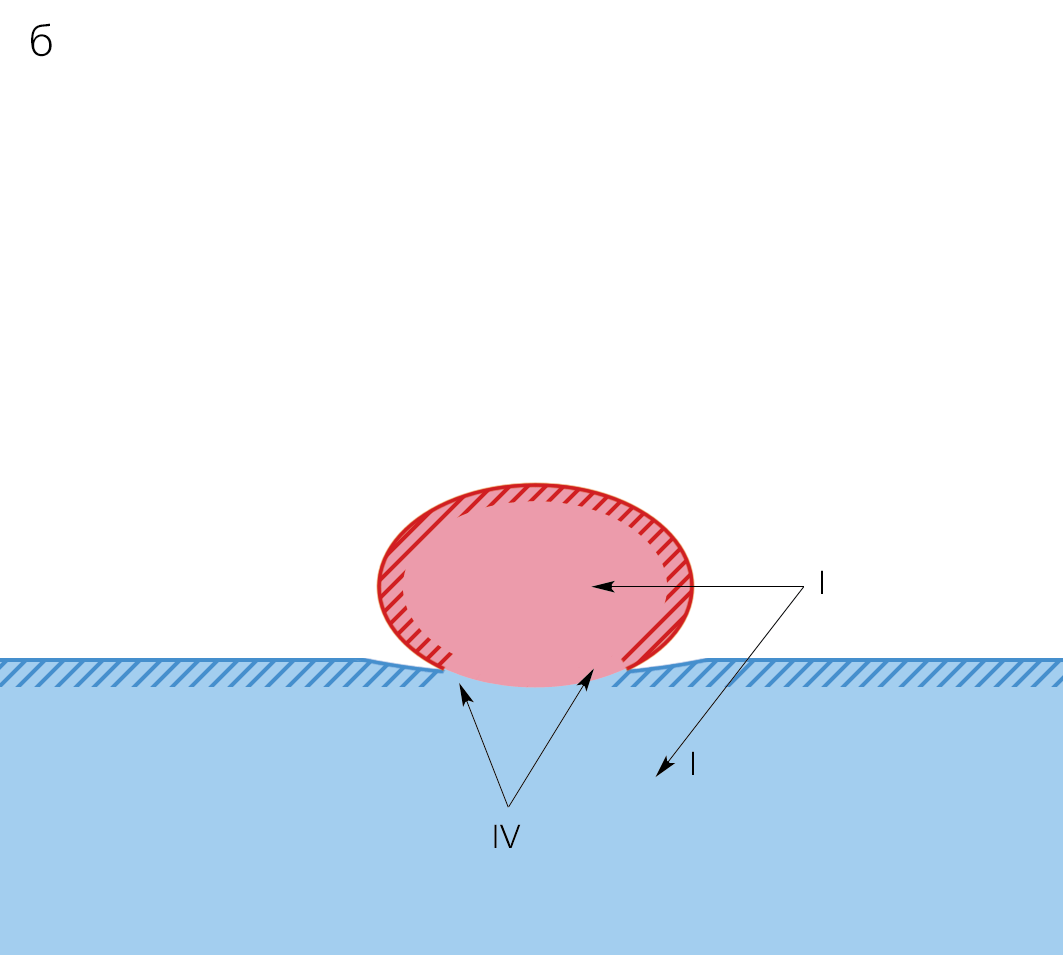
При первичном контакте капли, которая падает со скоростью ~1 м/с, с принимающей жидкостью молекулярный поверхностный слой уничтожается за время ~10-10 с, а приповерхностный толщиной δc — область первичного слияния IV — за ~10-8 с. Возникающий скачок давления складывается с давлением торможения и ускоряет тонкий слой слившихся жидкостей. Под действием избыточного давления, локализованного в тонкой области, формируется разлетающаяся пелена, и вещество капли разгоняется по дну каверны. Именно поэтому скорость капелек, вылетающих с вершин стримеров на кромке пелены, на порядок и более превосходит скорость падающей капли. Размеры области избыточного давления со временем увеличиваются, соответственно растут и толщина пелены, и диаметры капелек, все медленнее вылетающих с вершин стримеров.
При первичном контакте капли свободная поверхность III и слой II уничтожаются одновременно по всей площади пятна соприкосновения падающей капли и принимающей жидкости. На более поздних стадиях (продолжительностью более 10-4 с) доступная потенциальная поверхностная энергия из исчезающих приповерхностных слоев II преобразуется в возмущения давления, температуры и скорости в скользящем кольце контакта жидкостей (рис. 10,б).
Вначале внешняя кромка области слияния сред IV (кольцевая граница клиновидного слоя вытесняемого воздуха) быстро движется наружу, затем останавливается и после погружения половины капли начинает смещаться внутрь, к центру каверны. Здесь она контактирует с возмущенной средой (длительность процесса слияния капли составляет несколько миллисекунд). При этом в принимающей жидкости возникают интенсивные мелкомасштабные течения, определяющие формирование, отрыв и перемещения газовых пузырьков.
Сходные процессы происходят и при отрыве газовых пузырьков, когда освобождение доступной потенциальной поверхностной энергии происходит в смыкающихся конических областях, которые образовались после разрыва газовой перемычки [14]Прохоров В.Е., Чашечкин Ю.Д. Генерация звука при падении капли на поверхность воды // Акустический журнал. 2011. Т.57. №6. С.792–803. Основные различия параметров звуковых пакетов обусловлены вариациями размеров образующихся газовых полостей первоначально неправильной формы. При неизменных условиях оказываются разными одноименные свойства излучаемых акустических пакетов — амплитуда, частота заполнения, длительность, значения которых определяются геометрией контактирующих поверхностей и динамикой скрытых течений.
В целом попадающая в жидкость капля инициирует еще более сложный комплекс взаимосвязанных явлений — уничтожения, деформации, образования и уничтожения новых контактных поверхностей, формирования течений и вихрей, групп капиллярных и акустических волн. Одновременно в среде идут макро- и микроскопические процессы перераспределения вещества, переноса импульса, взаимной трансформации потенциальной, кинетической и внутренней энергии, каждый из которых характеризуется собственным набором пространственных и временных масштабов. Продолжительность быстрых процессов, в частности исчезновения свободных поверхностей, не превышает долей микросекунды. Высокая плотность энергии в тонких прослойках способствует формированию тонкоструктурных высокоскоростных течений в приповерхностном слое, опережающих более медленные течения увлеченной принимающей жидкости. Чередование быстрых и медленных струек проявляется в причудливости картин распределения вещества с выраженной волокнистой структурой.
Затухая, сравнительно медленные волновые и вихревые процессы оставляют в толще жидкости долгоживущие циркуляционные течения, постепенно преобразующие планарные приповерхностные структуры в трехмерные струйки, петли и вихревые кольца. После затухания быстрых компонент тонко структурированные картины распределения примесей перестраиваются в волокнистые трехмерные вихревые кольца, которые продолжают изучаться с середины XIX в. [1]Rogers W.B. On the formation of rotating rings by air and liquids under certain conditions of discharge // American Journal of Science and Arts. Second Series. 1858. V.26. №77. P.246–258.
* * *
В заключение хотелось бы выразить надежду, что автору удалось продемонстрировать тесные связи атомно-молекулярных и макроскопических процессов, завязанных в общий узел феноменом падающей капли. Гидродинамика и акустика последней представляются своего рода общедоступной лабораторией для детализации этих связей, дальнейшее изучение которых позволит решить важные теоретические и технологические проблемы.
Литература
- Rogers W.B. On the formation of rotating rings by air and liquids under certain conditions of discharge // American Journal of Science and Arts. Second Series. 1858. V.26. №77. P.246–258.
- Reynolds O. On the action of rain to calm the sea // Scientific Papers on Mechanical and Physical Subjects. 1900. V.1. P.86–88.
- Бэтчелор Дж. Введение в динамику жидкости. М., 1973.
- Христианович С.А., Родионов В.Н. О подъеме облака атомного взрыва. М., 1954 [отчет Акад. наук СССР, Ин-т хим. физики].
- Worthington A.M. The splash of the drop. Series «The romance of science». N.Y.; L., 1895 [последнее издание: Worthington A.M. The Splash of the Drop. Гамбург, 2012].
- Prosperetti A., Oguz H.N. The impact of drops on liquid surfaces and the underwater noise of rain // Annu. Rev. Fluid Mech. 1993. V.25. P.577–602.
- Franz G.J. Splashes as sources of sounds in liquids // J. Acoust. Soc. Amer. 1959. V.31. №8. P.1080–1096.
- Ильиных A.Ю., Чашечкин Ю.Д. Гидродинамика контакта падающей капли со свободной поверхностью жидкости // Известия РАН. Механика жидкости и газа. 2016. №2. С.3–12.
- Чашечкин Ю.Д. Структура и динамика природных течений: теоретическое и лабораторное моделирование // Актуальные проблемы механики. 50 лет Институту проблем механики им. А.Ю. Ишлинского РАН. М., 2015. С.63–78.
- Чашечкин Ю.Д., Прохоров В.Е. Структура первичного звукового сигнала при столкновении свободно падающей капли с поверхностью воды // ЖЭТФ. 2016. Т.149. №4. С.864–875.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т.6: Гидродинамика. М., 2006.
- Chashechkin Yu. D. Differential fluid mechanics — harmonization of analytical, numerical and laboratory models of flows // Mathematical Modeling and Optimization of Complex Structures. Springer Series «Computational Methods in Applied Sciences». 2016. V.40. P.61–91.
- Гиббс Дж.В. О равновесии гетерогенных веществ. Термодинамические работы. М.; Л., 1950.
- Прохоров В.Е., Чашечкин Ю.Д. Генерация звука при падении капли на поверхность воды // Акустический журнал. 2011. Т.57. №6. С.792–803.